
Ogden, Utah, USA
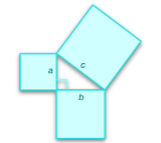
"Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity."
Angus K. Rodgers
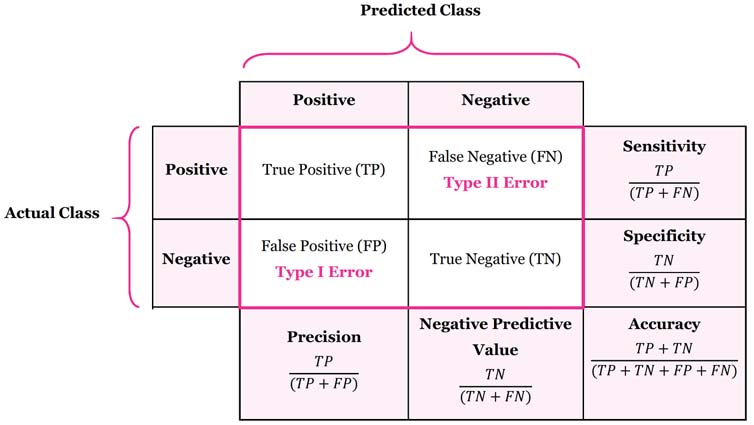
source
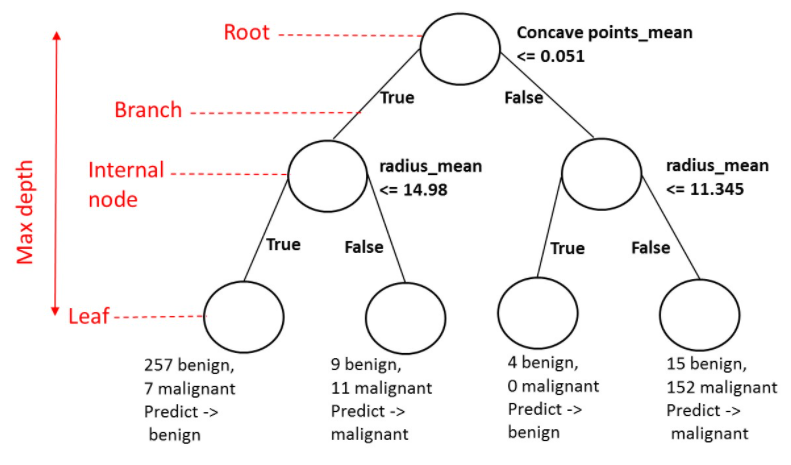
source
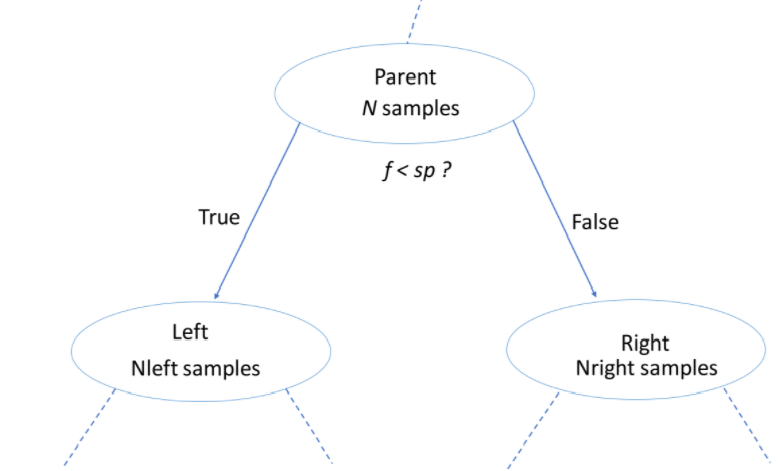
source
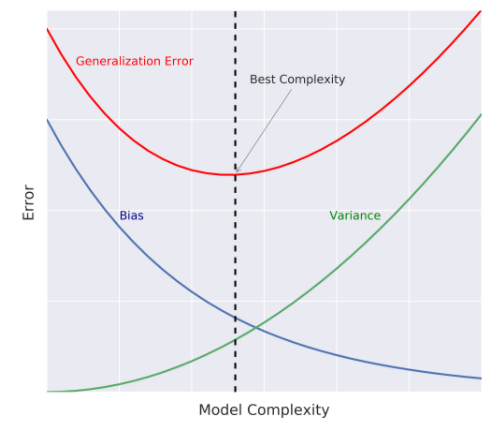
source
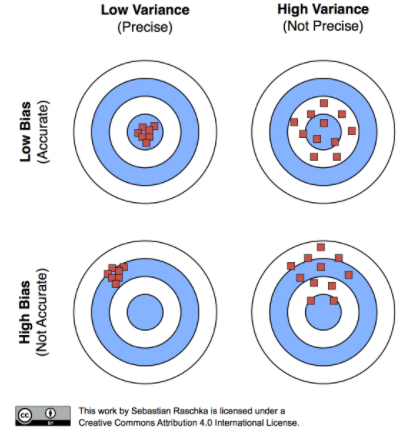
source
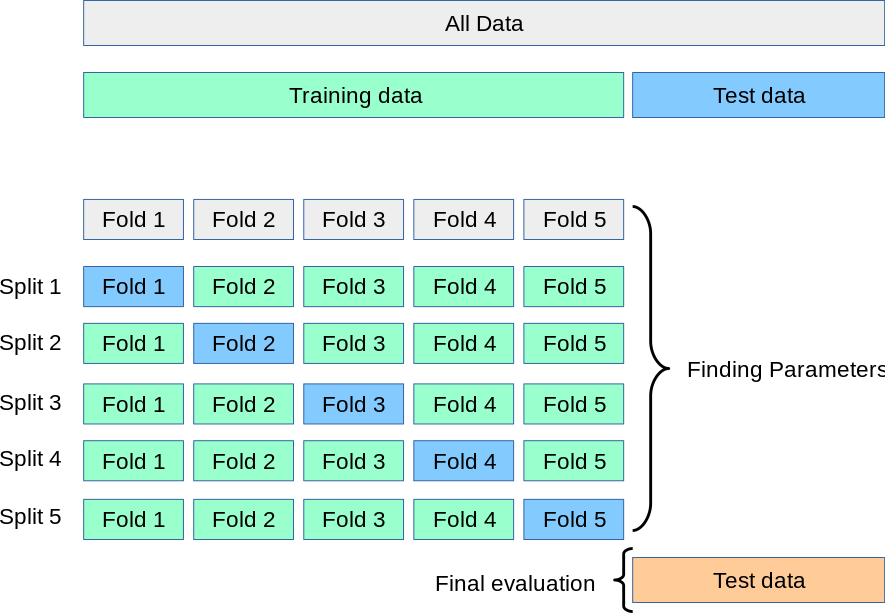
source
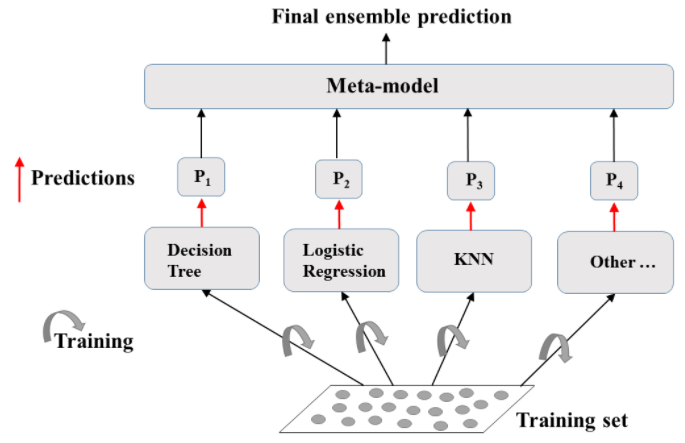
source
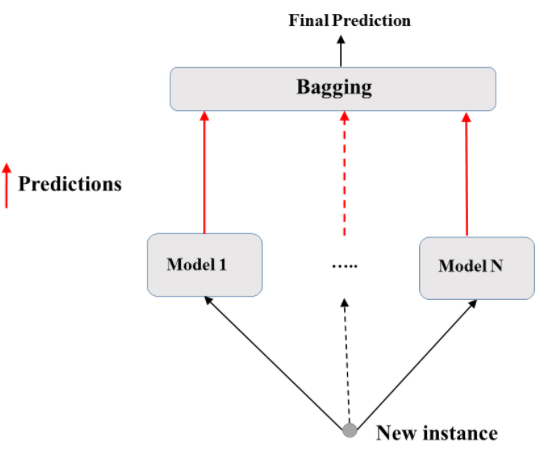
source
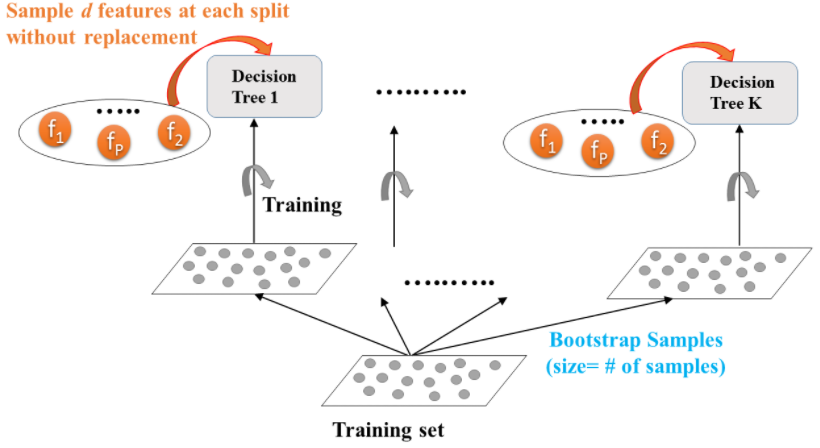
source
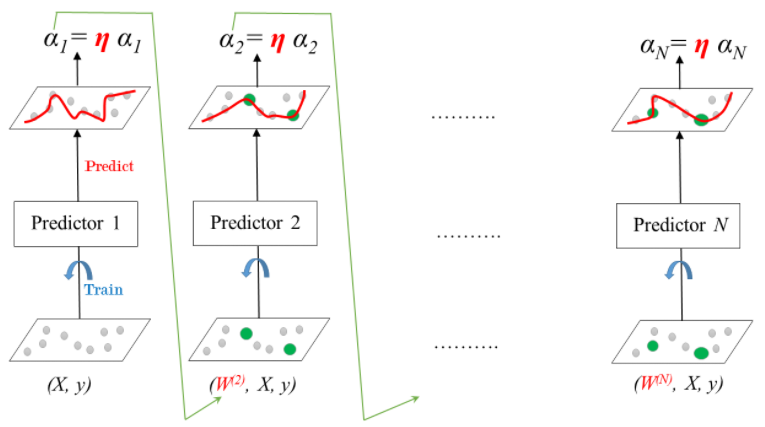
source
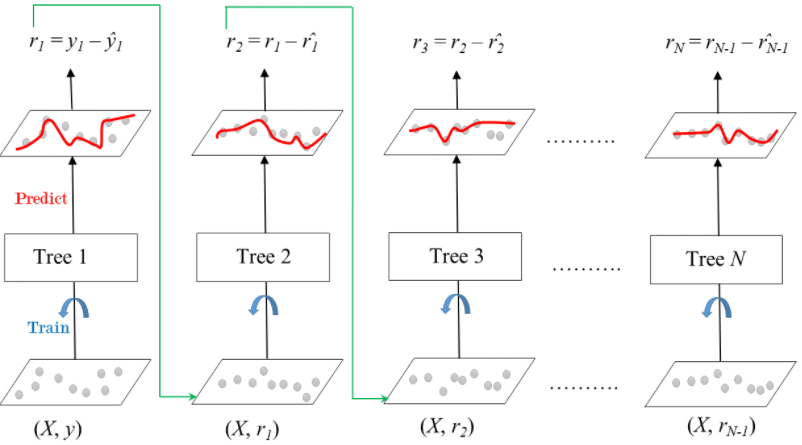
source
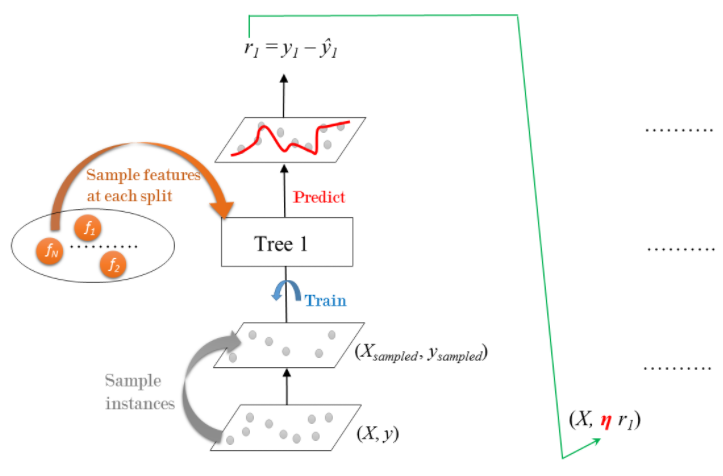
source
| v1 | v2 | v3 | |
|---|---|---|---|
| v1 | 1 | 0 | 0 |
| v2 | 0 | 1 | 0 |
| v3 | 0 | 0 | 1 |
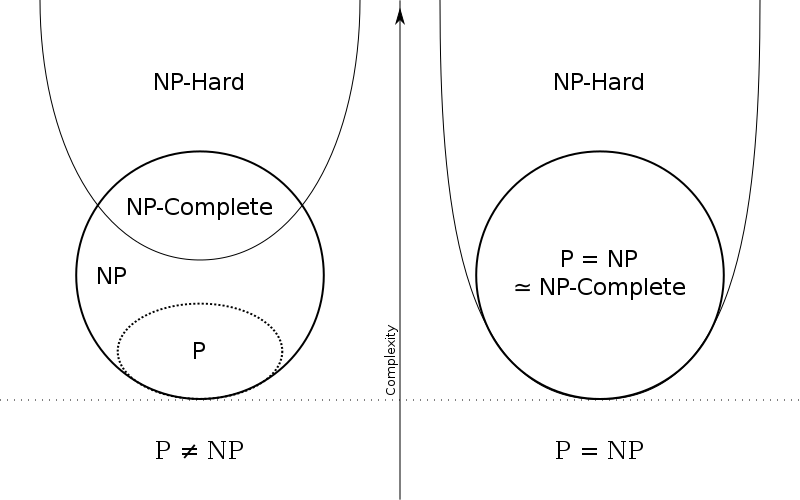
| p | q | p∧q | p∨q |
|---|---|---|---|
| T | T | T∧T = T | T∨T = T |
| T | F | T∧F = F | T∨F = T |
| F | T | F∧T = F | F∨T = T |
| F | F | F∧F = F | F∨F = F |
I am training as a Software Developer, Data Analyst & Machine Learning Engineer. I
am currently enrolled in the Software Technology program at Ogden-Weber Technical College. I am also
acquiring certifications as an ML Engineer & Algorithmic Trader from Udacity.
I have a Masters in Data Analytics, an MBA & an MS in Instructional Design. I have
working knowledge of C#, R, SQL, HTML, CSS, Javascript, Java and Python programming
languages.
I have a multi-displinary background including military intelligence,
psychology, linguistics, economics, virtual reality & educational technology. I have
worked abroad for ten years with military, universities & vocational schools.
I have working knowledge of Arabic, Chinese & French. I am very
mobile, able to relocate quickly, adapt easily to diverse working conditions
& have a current passport.
I have a passion for mathematics, statistics & artificial intelligence.
I am enthusiastic, highly self-motivated & enjoy presenting informative data
to decision makers. I am eager to work with dynamic teams to create
high quality products & services.